Yey for Fourier: Properties and Applications of the 2D Fourier Transform

ACTIVITY 6: Properties and Applications of the 2D Fourier Transform

-Jessica Nasayao

In this activity, our aim is to investigate the different properties of the Fourier transforms of different patterns and try to apply them to real world applications.

From the previous experiments, we were able to observe that the FT of a pattern inverts the pattern’s dimensions; e.g., what is narrow in the image’s axis will appear wide in it’s Fourier Transform, and vice versa. This property is called anamorphism. To demonstrate this property further, we applied FT to different patterns namely: a tall rectangle, a wide rectangle, and to two dots with varying spaces in between. The results are shown in the images below.

Figure 1. a) Wide rectangular pattern and b) its Fourier Transform

Figure 2 a) Tall rectangular pattern and b) its Fourier Transform

Figure 3 a) Two dots of relatively close spacing and b) its Fourier Transform

Figure 4 a) Two dots of relatively far spacing and b) its Fourier Transform

We can see that the bright bands of the tall rectangle’s Fourier transform lies along the x-axis, while those of the wide rectangle are on the y-axis. Taking the Fourier Transform of two bright dots placed closely together results in a corrugated roof of a small frequency. On the other hand, if placed far apart, the same bright dots will give a corrugated roof of a larger frequency.

Next, we want to know how rotating the patterns affects the Fourier transform. First, we get the Fourier Transform of a corrugated roof, as shown below.

 

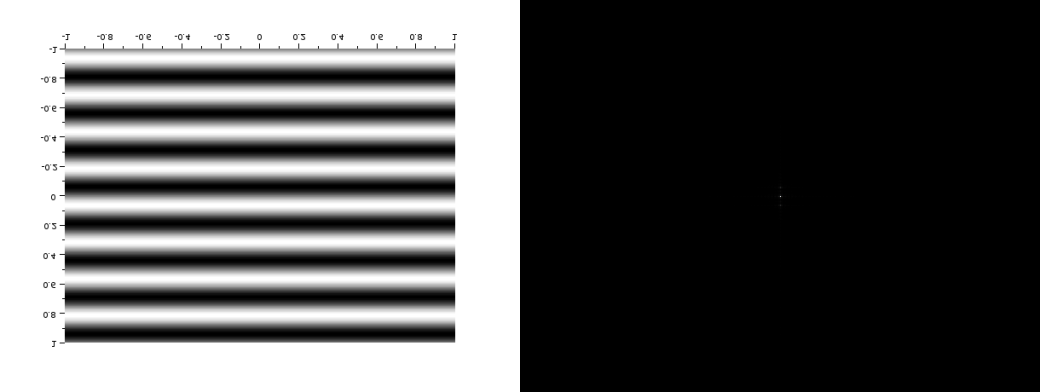
Figure 5 a) Corrugated roof of frequency 4 and b) its Fourier transform

 

Figure 6 a) Corrugated roof of frequency 10 and b) its Fourier transform

We can see that as the frequency increases, the dots in the Fourier tranform gets further away from each other.

If we rotate the corrugated roof, the Fourier transform pattern also rotates, as shown in the images below:

Figure 7 a) Corrugated roof rotated 30 degrees and b) its Fourier transform

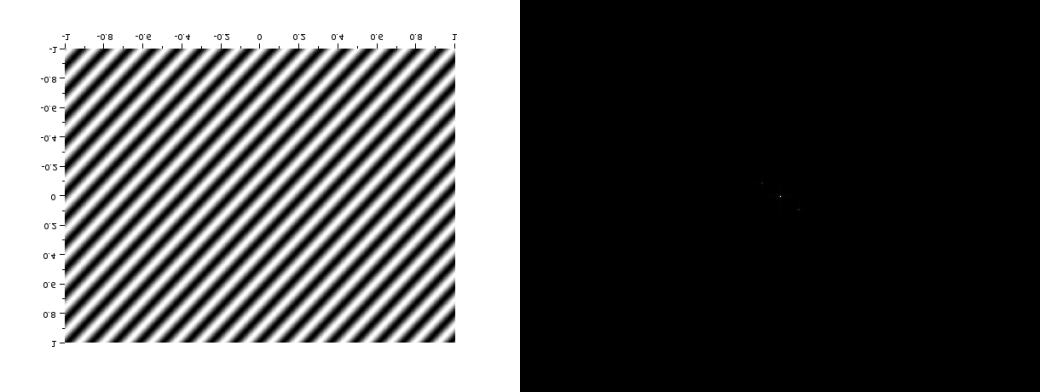
Figure 8 a) Corrugated roof rotated 120 degrees and b) its Fourier transform

If we try to synthesize a combination of sinusoids along the X and Y axes, the Fourier transform is also the combination of the individual Fourier transforms of the sinusoid, as shown in Figure 9.

Figure 9. a) Mix of corrugated roofs running along the X and Y axes and b) its Fourier Transform

 

If we add a rotated sinusoid to this synthetic pattern, the Fourier will also be the combination of the Fourier transforms of the three sinusoids. The image of the Fourier Transform is slightly blurry though, but if you look closely, you can make out the pattern.

 

Figure 10. a) Mix of sinusoids of different orientations b)its Fourier Transform

 

Earlier, we  displayed the Fourier transform of two dots along the x-axis, symmetric about the center. We also tried this on different patterns: two circles, two squares, and two Gaussians, and observed the results.

Figure 11. Fourier transform of two circles.

 

Figure 12. Fourier transform of two circles with a different radius.

 

Figure 13. Fourier transform of two squares.

Figure 14. Fourier transform of squares of a different size.

 

Figure 15. Fourier transform of two gaussians.

Figure 16. Fourier Tranform of two gaussians. (difference variance)

Now, what do you think will happen if we convolute a pattern to an image with randomly-positioned approximations of n dirac deltas? Turns out, the pattern will be repeated n times, each of themcentered on the dirac delta approximations, like the image below.

Figure 17. Dirac delta approximations.

Figure 18. Convolution with a small triangular pattern.

If we create an array of equally spaced dots along the x and y axes and take it’s Fourier transform, the result will look like the ones shown in the images below.

Figure 19. a) Equally spaced dots along the x and y axes b) its Fourier Transform

FIgure 20. a) Dots of different spacing b) its Fourier Transform

 

Now that we have already familiarized ourselves with the properties of Fourier transform, let’s try to use them in some real-world application. Consider, for example, this image of the moon:

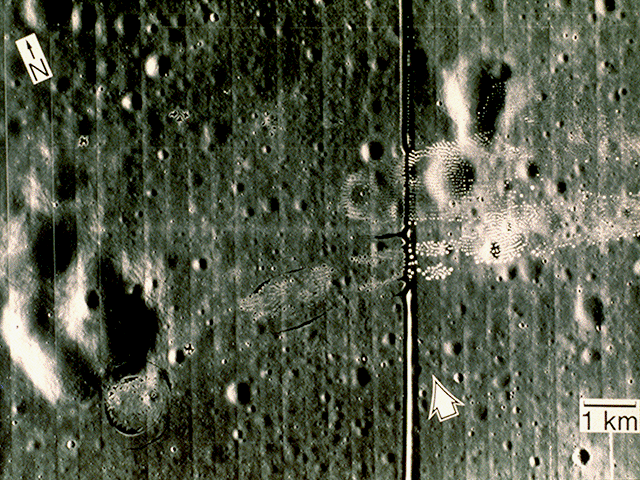
Figure 21. Picture of the moon.

If we take the Fourier transform of that image, we get the following result:

Figure 22. a) Grayscale of the image and b) its Fourier Transform

What we want to do is to try and see if we can remove the vertical and horizontal lines from the image. From the anamorphism property demonstrated earlier, we know that the horizonatal lines correspond to the vertical ones in the Fourier transform, and vice versa. We can try and make a mask such that these frequencies will be eliminated from our FT image and use inverse Fourier to revert back to the original image. The mask I used is shown below.

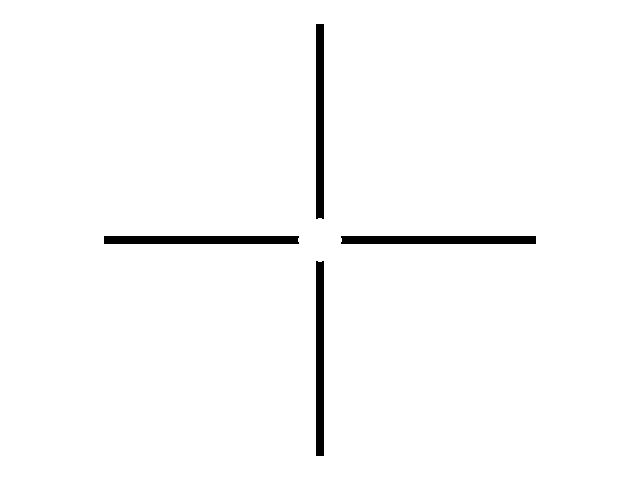
Figure 23. Mask used to eliminate vertical and horizontal lines in the image.

 

I convoluted this mask to the Fourier transform of my image and did an inverse fourier transform on the resulting matrix. The comparison between the original and the resulting image was shown below. The lines were visibly eliminated from the image.

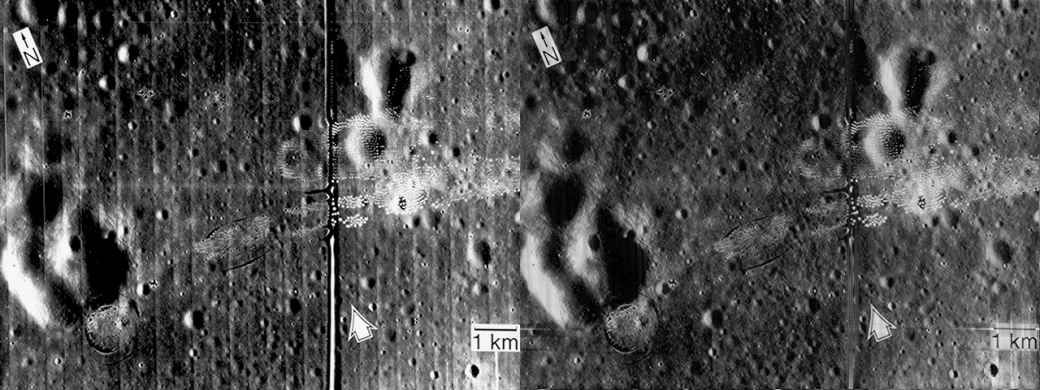
Figure 24. Comparison between the a) Original image and the b) result of the process.

We can apply the same logic to different images. Next, consider a scanned image of a fingerprint, shown below.

Figure 25. Scanned finger print. Image retrieved from: http://grupocasacam.com/covao/latent-fingerprints&page=5

Applying Fourier transformation to the image, we get:

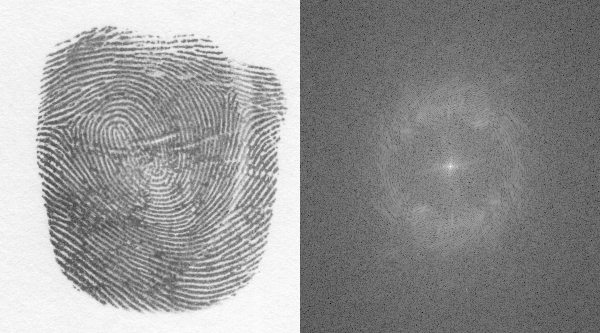
Figure 26. a) Grayscale of the fingerprint and the b) Log of its Fourier transform.

To eliminate the dark smudges of ink and hopefully enhance the ridges of our fingerprint, we use a mask that is produced by setting a threshold value on our FT image. The mask I used was shown below.

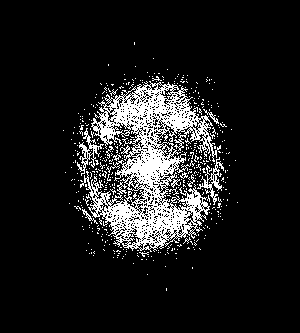
Figure 27. Mask used for ridge detection.

We now again apply the same process we did earlier and convolute this mask to the FT of our image. Shown below is the resulting image and its comparison to the original image after performing an inverse transform to the convoluted matrix. The blotches between ridges are visibly reduced and the ridges enhanced.

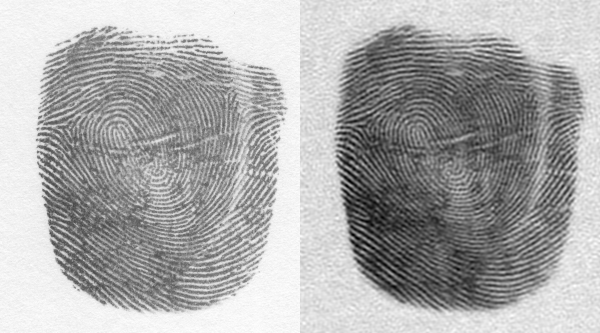
Figure 28. Image of the fingerprint a)Before ridge detection and processing and b) after processing.

 

---

Self-score: 10/12

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A day with Fourier: Fourier Transform Model of Image Formation

ACTIVITY 5: Fourier Transform Model of Image Formation

—Jessica Nasayao

First, I want to know what the Fourier transform of an image looks like. Starting with a circle, I proceeded to apply the FFT2 function (fft2) in Scilab to this image. However, FFT2 interchanges the quadrants along the diagonals, so I still need to interchange the quadrants back using fftshift. After doing this, I tried applying FFT2 twice to see if I could get the original image. Sure enough, doing so takes me back to the white circle, as shown in the image below.

Image of the circle after applying fft2, fftshift and fft2 again, respectively, from left to right.

So now we know how the Fourier transform works. But, the question now is, is the effect the same for images with no radial symmetry like the circle? To answer this question, we do the same thing to an image of the letter A. The results are shown below.

Image of the letter A after applying fft2, fftshift and fft2 again, respectively, from left to right.

Turns out, if you try to apply FFT2 to an image twice, it will give you the vertically flipped version of the original image.

Applying the Fourier transform to different synthetic images, we get the following results:

Here’s the snippet of code I used:

i=imread(“/home/jnasayao/Desktop/AP_186/Activity5/circle_act5.bmp”);
i= im2double(i);
shape = .299*i(:,:,1) + .587*i(:,:,2) + .114*i(:,:,3);
Fshape = fft2(shape);
ff_t = (mat2gray(abs(Fshape)));
ft_circle = mat2gray(fftshift(abs(Fshape)));
fft_circle = abs(fft2(Fshape));
img= [ff_t ft_circle fft_circle];
imwrite(img, “/home/jnasayao/Desktop/AP_186/Activity5/circle.png”);

The next question is: can we use the concept of Fourier Transform to simulate an imaging device? We know by the Convolution theorem that, if you get the linear transformation of two functions and convolve them, the result will be a function similar to its “parent” functions. Now, how do this concept apply to imaging? We can think of the two functions as the object and the camera lens, and the resulting convolution of their linear transformations as the image reproduced by the camera. We now try to simulate this by taking the Fourier transformation of an image and a white circle, the latter serving as the camera’s aperture, and convolving these two images. We get the following result:

                                     Aperture size and resulting convolved image.

The reproduced image becomes clearer as the aperture size gets larger. Shown below is the comparison between the original image and the result of convolution with the largest synthetic aperture.

Original image vs. Clearest convolved image.

Here’s the code I used for this part:

v = imread(“/home/jnasayao/Desktop/AP_186/Activity5/VIP_act5.bmp”);
a = imread(“/home/jnasayao/Desktop/AP_186/Activity5/aperture3_act5.bmp”);
vgray = double(rgb2gray(v));agray = double(rgb2gray(a));
Fv = fft2(vgray);
Fa = fftshift(abs(agray));
FAV = Fv.*(Fa);
IAV = fft2(FAV);
FImage = mat2gray(abs(IAV));
img = [vgray FImage];
imwrite(img, “/home/jnasayao/Desktop/AP_186/Activity5/comparison.png”);

Turns out, Fourier transform can be used for template matching, too! For example, if we want to find the position of occurrences of a letter in a sentence, we can get the Fourier transform of both the letter and the sentence images and multiply them element by element. In this case, I picked the letter A and generate a white image of it on a black background. Next, a sentence with the same font was constructed such that it contains the letter A . The FFT2 of the conjugate of the product of their fourier transforms gives us the following image:

Template matching.Bright dot s in the right picture suggests the position of the letter A.

The bright dots indicate the position of the letter A in the sentence image. Sure enough, these positions are where the A can be found.

The code I used for this part is shown below.

sp = imread(“/home/jnasayao/Desktop/AP_186/Activity5/RAIN_act5.bmp”);
a = imread(“/home/jnasayao/Desktop/AP_186/Activity5/ARAIN_act5.bmp”);
spgray = double(rgb2gray(sp));
agray = double(rgb2gray(a));
Fa = double(fft2(agray));
Fsp = double(fft2(spgray));
Fspa = conj(Fsp).*(Fa);
Ispa = fft2(Fspa);
Fimage = mat2gray(abs(fftshift(Ispa)));
img = [mat2gray(spgray) Fimage];
imwrite(img, “/home/jnasayao/Desktop/AP_186/Activity5/spain.png”)

Another application of Fourier Transform is edge detection. Apparently, if you convolve an image with a matrix whose sum of elements is zero, you get to see interesting images which vary according to the pattern of the matrix. Trying this on the previously generated VIP image, I was able to get the following resulting images:

Images generated when image is convoluted with a centered horizontal, centered vertical, diagonals and a spot pattern, from left to right respectively.

Here’s the snippet of code I used:

v = imread(“/home/jnasayao/Desktop/AP_186/Activity5/VIP_act5.bmp”);
vgray = double(rgb2gray(v));
pattern1 = [1 1 1; -2 -2 -2; 1 1 1];
pattern2 = [1 -2 1; 1 -2 1; 1 -2 1];
pattern3 = [-2 1 1; 1 -2 1; 1 1 -2];
pattern4 = [1 1 -2; 1 -2 1; -2 1 1];
pattern5 = [1 1 1; 1 -8 1; 1 1 1];
edge1 = conv2(vgray, pattern1);
edge2 = conv2(vgray, pattern2);
edge3 = conv2(vgray, pattern3);
edge4 = conv2(vgray, pattern4);
edge5 = conv2(vgray, pattern5);
img = [edge1 edge2 edge3 edge4 edge5];
imwrite(img, “/home/jnasayao/Desktop/AP_186/Activity5/edges.png”);

---

All in all, I would give myself a 9/10 on this one, since I think I’ve done quite good, being new to Scilab and all. 🙂

Green with envy: How to estimate area using Green’s theorem

Author’s Note: Hello readers! Today I shall show you how to estimate the area of an object using image processing. Think it doesn’t sound cool? Well, it is (If you are a geek like me, that is)! Just go on reading and maybe you’ll agree with me after. 🙂

---

ACTIVITY 4: Length and Area estimation

To get the area of an image, one can either treat the image as a blob and count the pixels in that blob, or do away with the tedious counting altogether and use Green’s theorem instead. If there are Nb pixels in the boundary of the region under consideration, then the area of the region, according to Green’s theorem is given by

Green’s Theorem in discrete form.

Okay, so what I want to do now is try to apply Green’s theorem and see how it works. First, I made a synthetic image of a white rectangle in a black background using scilab and used the scilab function edge to get the contour of my region:

Synthetic image of a rectangle.

Contour of the rectangular region.

Then I got the pixel coordinates of the edges and sorted it according to increasing polar angle. I then applied Green’s Theorem to get the area of the rectangular region. This value was then compared to the area obtained from counting the pixels in Scilab. The code I used for this activity is shown below:

shape=imread("/home/jnasayao/Desktop/AP_186/rect_act4.bmp");
shape=rgb2gray(shape);
edges = edge(shape, "prewitt");
[y,x] = find(edges);
x0 = median(x);
y0 = median(y);
X = x-x0;
Y = y-y0;
theta = atan(Y,X);
[theta, ind] = gsort(theta, 'g', 'i');
x($+1) = x(1); //loop back to first element
y($+1) = y(1);
ind($+1) = length(theta)+1;
summation = 0
for i = 1:length(theta)
    summation = summation + x(ind(i))*y(ind(i+1)) - y(ind(i))*x(ind(i+1))    
end

exp_area=summation*0.5;

theo_area= length(find(shape==255))
disp(theo_area)
disp(exp_area)
percent_error= (theo_area-exp_area)*100/theo_area
disp(percent_error)

The area calculated using Green’s theorem yields a 1.42% error when compared to the area obtained from counting the pixels of the region. So far, so good.

Next, I tried to apply this method to real world objects. I first obtained an image of the Smart-Araneta Coliseum from Google maps:

Satellite image of Smart-Araneta Coliseum from Google Earth.

I then used GIMP to create a binary image of the Coliseum’s roof which I will define as my region R.

Binary image of the Coliseum’s roof.

I proceeded to calculate the area of this region using the method described above and got a 2.47% error when I compared the calculated area from the analytical area. Using the scale provided by Google, I was able to get a conversion factor of 0.35 sq meter/pixel, and, multiplying this to the pixel count, I was able to calculate a total area of  27, 942 square meters, which yields a 21.49% error from the expected floor area of 23, 000 square meters. I guess the error comes from the fact that I measured the roof instead of the floor (since of course I don’t have a choice; I would need to remove the dome’s roof to get a satellite image of the floor lol) and of course, this is bound to give me discrepancies.

---

All in all I would give myself 8/10 for this activity, since I think I did fairly good enough, being a newbie in Scilab and all. 🙂 Cheers!

Starting with the basics: To Scilab and beyond!

Author’s Note: Being a Python programmer, I must admit I had some qualms about doing image processing in Scilab. First of all, I have zero knowledge in the language, and second, I didn’t think I can learn everything I need in time to finish the required activities. Doing the activities in Python seems to be the best choice. Despite these doubts, however, I still downloaded Scilab. And boy, did it make my life much easier! Turns out Scilab is specifically designed to handle matrices, which is an essential (if not vital) part of image processing. And that is how I learned a new programming language!

—Jessica T. Nasayao

---

ACTIVITY 3: Scilab Basics

For the this activity, we were tasked to construct synthetic images of the following: a centered square aperture, a sinusoid along the x-direction (corrugated roof), a grating along the x direction, an annulus, a circular aperture with graded transparency, an ellipse, and a cross-shaped aperture. I used Scilab to plot the images mentioned.

For the square aperture, two 2D arrays corresponding to the x and y axes of the graph were first constructed. A zero matrix was then made, with the same shape as the X and Y matrices. A certain number was set, and for values in the X and Y arrays less than the absolute value of this number, the corresponding index in the zero matrix was set to a value of 1. In this manner, I was able to synthesize a square aperture.

nx = 1000; ny = 1000;
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
A = zeros(nx,ny);
A(find(abs(Y)<0.4 & abs(X)<0.4)) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Figure 1. Synthesized square aperture.

The sinusoid along the x-direction, however, was constructed in a different way. Instead of constructing a zero matrix, the sine values of the X 2D array was directly calculated and plotted.

nx = 1000; ny = 1000;
x = linspace(-8*%pi,8*%pi,nx);
y = linspace(0,1,ny);
[X] = ndgrid(x,y);
r = sin(X);
f = scf();
grayplot(x,y,r);
f.color_map = graycolormap(32);

Figure 2. Synthesized corrugated roof image.

The grating along the x-direction was easily synthesized by getting the values of the X 2D array when plugged in a square function. The resulting values was directly plotted. The built-in square function in Scilab was used.

nx = 1000; ny = 1000;
x = linspace(0,50*%pi, nx);
y = linspace(-1,1,ny);
[X] = ndgrid(x,y);
A = zeros(nx,ny);
r = squarewave(X);
f = scf();
grayplot(x,y,r);
f.color_map = graycolormap(32);

Figure 3. Synthesized grating along the x-direction.

An annulus was constructed by again defining a zero matrix similar in shape with the X and Y 2D arrays. The equation (x-a)² + (y-b)² = r² defining a circle centered on cartesian coordinates (a,b) was then used to define a matrix r. A zero matrix was defined, and for each element of the matrix r between a set range, the corresponding matrix element in the zero matrix was set to 1.

nx = 1000; ny = 1000; 
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
r= sqrt(X.^2 + Y.^2);
A = zeros (nx,ny);
A (find(r<0.7 & r>0.5) ) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Figure 4. Synthesized annulus.

For the circular aperture with graded transparency, the X and Y array values were directly plugged to a 2D gaussian function.

nx = 1000; ny = 1000;
x = linspace(-5,5,nx);
y = linspace(-5,5,ny);
[X,Y] = ndgrid(x,y);
r = exp(-(((X.^2)+(Y.^2)/2)));
f = scf();
grayplot(x,y,r);
f.color_map = graycolormap(32);

Figure 5. Synthesized circular aperture with gaussian transparency.

The elliptical aperture was likewise constructed by plugging the  and Y 2D arrays into the equation of the ellipse defined as r in the code below. For values greater than a set number, the corresponding element in the zero matrix was set to 1 as shown:

nx = 1000; ny = 1000;
x = linspace(-5,5,nx);
y = linspace(-5,5,ny);
[X,Y] = ndgrid(x,y);
r = ((X.^2)/3^2) + ((Y.^2)/1)
A = zeros(nx,ny);
A(find(r<0.5)) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Figure 6. Synthesized elliptical aperture.

Lastly, the cross aperture was synthesized by constructing two overlapping rectangular apertures, as shown in the code below:

nx = 1000; ny = 1000;
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
A = zeros(nx,ny);
A(find(abs(Y)<0.6 & abs(X)<0.3)) = 1;
A(find(abs(Y)<0.3 & abs(X)<0.6)) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Figure 7. Synthesized cross-shaped aperture.

---

Since I really thought I did my best in this activity, I thought I’ll give myself a 10/10. 😀

The world of image processing: Digital Scanning and Reconstruction

Author’s Note: Hello readers! I am Jessica, a senior physics student from the University of the Philippines. This blog was made to keep record of my first venture into the world of image processing. I hope you enjoy reading the articles as much as I enjoyed writing them!

—Jessica T. Nasayao

---

Activity 2: Digital Scanning

For this activity, we were tasked to scan a hand-drawn graph from old books (in my case, I used an old thesis) and try to reconstruct the graph using ratio and proportion. The scanned picture of the graph I obtained was shown below:

Figure 1. Scanned graph

The scanned image was opened in GIMP. Using the pointer dialog, the corresponding pixel positions of the x and y ticks were obtained. From this, two graphs were constructed, and a linear relationship between the pixel positions and tick marks is obtained for both x and y axes , as shown below:

Figure 2. Pixel positions of x ticks

Figure 3. Pixel positions of y ticks.

The equations obtained from these graphs were then used to calculate the values of the points from their pixel positions in the graph. By doing this, I was able to reconstruct the plot (Yehey!). The reconstructed graph and the scanned image were superimposed in the figure below.

Figure 4. Reconstructed graph with the scanned graph in the background.

---

That was fairly easy, and I think I did a good job in reconstructing the graph! I think I’ll give myself a 10/10. 😀

Hello world!

This is your very first post. Click the Edit link to modify or delete it, or start a new post. If you like, use this post to tell readers why you started this blog and what you plan to do with it.

Happy blogging!